Factorials - A Look At Infinity. | BRAINTENANCE: Train, Strain And Improve Your Brain. Expand Your Mind.

Monday, July 8, 2013

Factorials - A Look At Infinity.

Share this ARTICLE with your colleagues on LinkedIn .

If I asked you for the sum of the integers from 1 to 100 inclusive, you could solve the problem by an easy formula [ref.: formula for the sum of an arithmetic series]. But if I asked you for the product of all of the integers from 1 to 100 (or 100!, as this is written), if you didn't have a shortcut you'd come back to me 3 days and several gallons of Red Bull [I hate the stuff] later -- and odds are, if you did the calculation manually, you've introduced at least one error, which makes your result a study in 1) discipline and devotion; and 2) high unreliability.

Happily, over the years, mathematicians have pondered this problem and found a formula to approximate the result. Note that the factorial formula is increasingly accurate as the amount of numbers multiplied grows, i.e., the formula would be rotten for calculating 10!, poor for 100!, passable for 1,000! and very darn close and useful for 10,000! Now "here", as the ignorami [a Lingovation of the highest order, and not to be confused with the Order Of The Illuminati, lest they get ticked off and do terrible things to you -- like having you mentioned in a Dan Brown -- uggggh -- novel] amongst us are wont to say, is "the beauty part":

Calculating factorials

The numeric value of n! can be calculated by repeated multiplication if n is not too large. That is basically what pocket calculators do. The largest factorial that most calculators can handle is 69!, because 70! > 10100.

When n is large, n! can be estimated quite accurately using Stirling's approximation: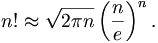

You can actually do the above (if you are lazy, as I am), by using a generator available right on the internet!***

Where Pi = Fraction: 22/7. Decimal: 3.14 - or - 3.141592653589793238462643... and,

Where e = 2.71828

___________________________________________________________________________

Factorials can be useful to facilitate expression manipulation. For instance the number of k-permutations of n can be written as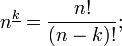

while this is inefficient as a means to compute that number, it may serve to prove a symmetry property of binomial coefficients:

Okay, Braintenancers, Mind Expanders, Brain Trainers, And Cognition Expanders:

Here is a generator which you can use to further shortcut Stirling's brilliant (but still somewhat hairy) formula:

Click on either of these little mamas and simply plug in your data:

http://www.nitrxgen.net/factorialcalc.php

http://www.kalkulacka-online.com/faktorial.php?l=en

As always, thank you for reading me, and for sharing my articles with your colleagues and connections across your social media platforms using you ever-increasing collection of social media sharing tools.

Douglas E. Castle

Sponsored By:
CFI - CrowdFunding Incubator LLC
ICS - International Connection Services
Global Edge Technologies Group LLC
CFI Business Growth
Douglas E. Castle On LinkedIn - Join Me!